1. Algoritma Floyd-Warshall
Algoritma
floyd-warshall adalah satu varian dari pemrograman dinamis,yaitu dengan
memandang solusi yang akan diperoleh sebagai suatu keputusan yang saling
terkait. Sehingga solusi solusi tersebut terbentuk dari solusi yang berasal
dari tahap seblumnya.Algoritma warshall ini berbeda dengan algoritma
greedy.karena algoritma greedy tidak diperhatikan konsekuensi yang akan terjadi
seandainya kita memilih suatu keputusan pada suatu tahap. Algoritma warshall
disebut juga algoritma dinamis.
karakteristik dari algoritma dinamis ialah :
1. persoalannya dibagi atas beberapa tahap,yang setiap tahapnya diambil satu keputusan.
2. Masing-masing tahap terdiri dari sejumlah status yang saling berhubungan.
3. Hasil keputusan akan di transformasikan.
4. Ongkos tergantung dari ongkos tahapan yang telah berjalan dan ongkos pada tahap itu sendiri.
5. Keputusan terbaik pada tahap bersifat independen.
6. Terdapat hubungan rekursif yang menyatakan bahwa keputusan terbaik dalam setiap status pada tahap -k.
Pada algoritma ini dilakukan pendekatan ,yaitu pendekatan maju dan pendekatan mundur.
karakteristik dari algoritma dinamis ialah :
1. persoalannya dibagi atas beberapa tahap,yang setiap tahapnya diambil satu keputusan.
2. Masing-masing tahap terdiri dari sejumlah status yang saling berhubungan.
3. Hasil keputusan akan di transformasikan.
4. Ongkos tergantung dari ongkos tahapan yang telah berjalan dan ongkos pada tahap itu sendiri.
5. Keputusan terbaik pada tahap bersifat independen.
6. Terdapat hubungan rekursif yang menyatakan bahwa keputusan terbaik dalam setiap status pada tahap -k.
Pada algoritma ini dilakukan pendekatan ,yaitu pendekatan maju dan pendekatan mundur.
Analisisnya :
Melakukan perbandingan terlebih dahulu,yaitu pada tiap tahap antara 2 simpul hingga perkiraan tersebut diketahui sebagai nilai optimal. Ada 2 kemungkinan yang terjadi jika kita mencari jalur terpendek (shortest path) dari setiap i ke simpul j dan perantara simpul 1 s.d ke k+1,
1. Jalur terpendek hanya berasal dari simpul yang berada antara 1 hingga k.
2. Ada sebagian jalur yang berasal dari simpul 1 s/d k+1 dan juga dari k+1 hingga i.
Maka dari itu rumus fungsi shortest path dengan algoritma ini ;
basis -0
shortest path(i,j,0)=edgecost(i,j);
rekurens
shortest path (i,j,k) = min(shortestpath (i,,j,k-1),shortestpath(i,k,k-1)+shortestpath(k,j,k-1);
Melakukan perbandingan terlebih dahulu,yaitu pada tiap tahap antara 2 simpul hingga perkiraan tersebut diketahui sebagai nilai optimal. Ada 2 kemungkinan yang terjadi jika kita mencari jalur terpendek (shortest path) dari setiap i ke simpul j dan perantara simpul 1 s.d ke k+1,
1. Jalur terpendek hanya berasal dari simpul yang berada antara 1 hingga k.
2. Ada sebagian jalur yang berasal dari simpul 1 s/d k+1 dan juga dari k+1 hingga i.
Maka dari itu rumus fungsi shortest path dengan algoritma ini ;
basis -0
shortest path(i,j,0)=edgecost(i,j);
rekurens
shortest path (i,j,k) = min(shortestpath (i,,j,k-1),shortestpath(i,k,k-1)+shortestpath(k,j,k-1);
pengertian dari
wikipedia :
Algoritma Floyd-Warshall memiliki input graf berarah dan berbobot (V,E), yang berupa daftar titik (node/vertex V) dan daftar sisi (edge E). Jumlah bobot sisi-sisi pada sebuah jalur adalah bobot jalur tersebut. Sisi pada E diperbolehkan memiliki bobot negatif, akan tetapi tidak diperbolehkan bagi graf ini untuk memiliki siklus dengan bobot negatif. Algoritma ini menghitung bobot terkecil dari semua jalur yang menghubungkan sebuah pasangan titik, dan melakukannya sekaligus untuk semua pasangan titik. Algoritma ini berjalan dengan waktu Θ(|V|3).
Algoritma Floyd-Warshall memiliki input graf berarah dan berbobot (V,E), yang berupa daftar titik (node/vertex V) dan daftar sisi (edge E). Jumlah bobot sisi-sisi pada sebuah jalur adalah bobot jalur tersebut. Sisi pada E diperbolehkan memiliki bobot negatif, akan tetapi tidak diperbolehkan bagi graf ini untuk memiliki siklus dengan bobot negatif. Algoritma ini menghitung bobot terkecil dari semua jalur yang menghubungkan sebuah pasangan titik, dan melakukannya sekaligus untuk semua pasangan titik. Algoritma ini berjalan dengan waktu Θ(|V|3).
Implementasi
algoritma ini dalam pseudocode: (Graf direpresentasikan sebagai matrix
keterhubungan, yang isinya ialah bobot/jarak sisi yang menghubungkan tiap
pasangan titik, dilambangkan dengan indeks baris dan kolom) (Ketiadaan sisi
yang menghubungkan sebuah pasangan dilambangkan dengan Tak-hingga)
function fw( int [1..n,1..n] graph) { // Inisialisasi var int [1..n,1..n] jarak := graph var int [1..n,1..n] sebelum for i from 1 to n for j from 1 to n if jarak[i,j] jarak[i,k] + jarak[k,j] jarak[i,j] = jarak[i,k] + jarak[k,j] sebelum[i,j] = sebelum[k,j] return jarak }
function fw( int [1..n,1..n] graph) { // Inisialisasi var int [1..n,1..n] jarak := graph var int [1..n,1..n] sebelum for i from 1 to n for j from 1 to n if jarak[i,j] jarak[i,k] + jarak[k,j] jarak[i,j] = jarak[i,k] + jarak[k,j] sebelum[i,j] = sebelum[k,j] return jarak }
2. Algoritma Bellman-Ford
Algoritma Bellman-Ford menyelesaikan masalah garis terpendek single-source untuk grafik dengan dua simpul(node) positive and negative. Jika kamu hanya membutuhkan untuk menyelesaikan masalah jalur terpendek untuk node positive, Algoritma Dijkstra memberikN lternatif yg lebih efisien. Jika semua node sama BFS adalah alternative yang lebih efisien.
Algoritma Bellman-Ford menyelesaikan masalah garis terpendek single-source untuk grafik dengan dua simpul(node) positive and negative. Jika kamu hanya membutuhkan untuk menyelesaikan masalah jalur terpendek untuk node positive, Algoritma Dijkstra memberikN lternatif yg lebih efisien. Jika semua node sama BFS adalah alternative yang lebih efisien.
Sebelum memanggil
fungsi bellman_ford_shortest_paths(),user harus menentukan puncak/root-nya
dengan nilai 0 atau ∞ tergantung user ingin memulai dengan node pertama yang
mana. Algoritma Bellman-Ford memproses dengan looping semua node di grafik,
menggunakan operasi relaksasi untuk setiap node. Pada pseucode di bawah ini, v
adalah puncak/root untuk u, w peta node, dan d adalah panjang peta yang merekam
panjang dari jalur terpendek untuk setiap node. Jika p adalah prosesor yang
telah direkam untuk parent dari setiap node, maka akan menjadi parent dari
pohon tersebut.
RELAX(u, v, w, d, p)
if (w(u,v) + d[u]
<>
d[v] := w(u,v) + d[u]
p[v] := u
else
…
relax edge (u,v)
edge (u,v) is not
relaxed
Algoritma akan
mengulang loop |V| kali setelah dijamin bahwa panjang dari setiap node telah
ditentukan kemungkinan minimum kalau grafik adalah rute negative. Jika grafik
adalah route negative, maka node di grafik tidak dapat di minimaliskan. Dalam
grafik aka nada node (u,v) seperti w(u,v) + d[u] <>
BELLMAN-FORD(G)
// Optional
initialization
for setiap root u di
V
d[u] := infinity
p[u] := u
end for
for i := 1 to |V|-1
for setiap node (u,v)
di E
RELAX(u, v, w, d, p)
end for
end for
for setiap node (u,v)
di E
if (w(u,v) + d[u]
<>
return (false, , )
else
…
end for
return (true, p, d)
Node uji (u,v)
node (u,v) tidak
diminimalis
node (u,v)
diminimalis
Ada dua pilihan utama
untuk memperoleh output dari fungsi Bellman. Jika user memberikan jarak peta
melalui parameter distance_map() kemudian jarak yang paling pendek dari node
utama untuk setiap root di grafik akan direkam dip peta jarak (diberikan jika
fungsi bernilai true). Pilihan kedua adalah merekam jalur pohon terpendek di
predecessor_map(). Untuk setiap root u di V, p[u] akan menjadi predesesor dari
u di jarak terpendek pohon (kalau tidak p[u] = u, pada kasus u adalah root
utama).Pada dua pilihan tersebut, user dapat memberikan pengunjung buatan
sendiri yang dapat mengambil aksi pada setiap poin dari kebanyakan algoritma.
pengertian dari
Wikipedia :
Algoritma Bellman-Ford menghitung jarak terpendek (dari satu sumber) pada sebuah digraf berbobot. Maksudnya dari satu sumber ialah bahwa ia menghitung semua jarak terpendek yang berawal dari satu titik node. Algoritma Dijkstra dapat lebih cepat mencari hal yang sama dengan syarat tidak ada sisi (edge) yang berbobot negatif. Maka Algoritma Bellman-Ford hanya digunakan jika ada sisi berbobot negatif.
Algoritma Bellman-Ford menghitung jarak terpendek (dari satu sumber) pada sebuah digraf berbobot. Maksudnya dari satu sumber ialah bahwa ia menghitung semua jarak terpendek yang berawal dari satu titik node. Algoritma Dijkstra dapat lebih cepat mencari hal yang sama dengan syarat tidak ada sisi (edge) yang berbobot negatif. Maka Algoritma Bellman-Ford hanya digunakan jika ada sisi berbobot negatif.
Algoritma
Bellman-Ford menggunakan waktu sebesar O(V.E), di mana V dan E adalah banyaknya
sisi dan titik.
Algoritma Semut
Algoritma semut diperkenalkan oleh Moyson dan Manderick dan secara meluas dikembangkan
oleh Marco Dorigo, merupakan
teknik probabilistik untuk menyelesaikan masalah komputasi dengan menemukan
jalur terbaik melalui grafik. Algoritma ini terinspirasi oleh perilaku semut dalam menemukan jalur dari
koloninya menuju makanan.
Pada dunia nyata,
semut berkeliling secara acak, dan ketika menemukan makanan mereka kembali ke
koloninya sambil memberikan tanda dengan jejak feromon.
Jika semut-semut lain menemukan jalur tersebut, mereka tidak akan bepergian
dengan acak lagi, melainkan akan mengikuti jejak tersebut, kembali dan
menguatkannya jika pada akhirnya merekapun menemukan makanan.
Seiring waktu,
bagaimanapun juga jejak feromon akan menguap dan akan mengurangi kekuatan daya
tariknya. Lebih lama seekor semut pulang pergi melalui jalur tersebut, lebih
lama jugalah feromon menguap. Sebagai perbandingan, sebuah jalur yang pendek
akan berbaris lebih cepat, dan dengan demikian kerapatan feromon akan tetap
tinggi karena terletak pada jalur secepat penguapannya. Penguapan feromon juga
mempunyai keuntungan untuk mencegah konvergensi pada penyelesaian optimal
secara lokal. Jika tidak ada penguapan sama sekali, jalur yang dipilih semut
pertama akan cenderung menarik secara berlebihan terhadap semut-semut yang
mengikutinya. Pada kasus yang demikian, eksplorasi ruang penyelesaian akan
terbatasi.
Oleh karena itu,
ketika seekor semut menemukan jalur yang bagus (jalur yang pendek) dari koloni
ke sumber makanan, semut lainnya akan mengikuti jalur tersebut, dan akhirnya
semua semut akan mengikuti sebuah jalur tunggal. Ide algoritma koloni semut
adalah untuk meniru perilaku ini melalui 'semut tiruan' berjalan seputar grafik
yang menunjukkan masalah yang harus diselesaikan.
Algoritma optimisasi
koloni semut telah digunakan untuk menghasilkan penyelesaian yang mendekati
optimal pada masalah salesman yang melakukan perjalanan. Algoritma semut lebih
menguntungkan daripada pendekatan penguatan tiruan (simulaten annealing) dan algoritma
genetik saat grafik mungkin berubah secara dinamis; algoritma
koloni semut dapat berjalan secara kontinyu dan menyesuaikan dengan perubahan
secara waktu nyata (real time). Hal ini menarik dalam routing jaringan dan sistem transportasi
urban.
Algoritma Genetika
Algoritma
Genetika adalah salah satu algoritma metaheuristic yang biasa digunakan untuk
melakukan pencarian solusi yang paling optimal (maximize atau minimize). Cara
kerja algoritma ini mensimulasikan fenomena dari evolusi alam. Intinya adalah,
spesies yang paling unggul akan memiliki kesempatan untuk bertahan hidup yang
lebih besar.
Konsep
dasar algoritma ini sebenarnya sederhana. Kromoson merepresentasikan sebuah
solusi potensial terhadap sebuah masalah. Proses pencarian solusi potensial
berikutnya dapat dibayangkan sebagai sebuah proses evolusi terhadap populasi
dari kromosom.
Pada
saat proses pencarian solusi potensial berikutnya, algoritma ini akan
menselaraskan dua tujuan:
- Eksploitasi
solusi-solusi terbaik
- Eksplorasi
ruang pencarian
Keromantisan
algoritma genetika terletak pada dua tujuan tersebut. Eksplorasi ruang
pencarian ibaratnya seseorang yang sedang mencari pasangan. Dia akan memperluas
“ruang pencarian” ketika dalam proses pencarian, tapi ketika sudah menemukan
yang cocok, dia akan fokus terhadap yang satu itu dan “mengeksploitasi” (dalam
arti mencoba lebih mengenal) pasangannya tersebut.
Tapi
tentunya analogi tersebut tidak sepenuhnya cocok di dunia nyata. Karena,
algoritma genetika akan terus mencari pada ruang pencarian, walau sudah
menemukan solusi potensial, sampai menemukan kondisi berhenti.
Sumber
LOGIKA
DAN ALGORITMA
Logika
Logika
berasal dari bahasa Yunani yaitu LOGOS yang berarti ilmu. Logika pada
dasarnya filsafat berpikir. Berpikir berarti melakukan suatu tindakan
yang memiliki suatu tujuan. Jadi pengertian Logika adalah ilmu berpikir
/ cara berpikir dengan berbagai tindakan yang memiliki tujuan tertentu.
berasal dari bahasa Yunani yaitu LOGOS yang berarti ilmu. Logika pada
dasarnya filsafat berpikir. Berpikir berarti melakukan suatu tindakan
yang memiliki suatu tujuan. Jadi pengertian Logika adalah ilmu berpikir
/ cara berpikir dengan berbagai tindakan yang memiliki tujuan tertentu.
Algoritma
Pada
Merriam-Webster’s Collegiate Dictionary, istilah algoritma diartikan
sebagai prosedur langkah demi langkah untuk memecahkan masalah atau
menyelesaikan suatu tugas. Kamus Besar Bahasa Indonesia (KBBI) mendefinisikan
algoritma sebagai urutan logis pengambilan keputusan untuk pemecahan
masalah.
Merriam-Webster’s Collegiate Dictionary, istilah algoritma diartikan
sebagai prosedur langkah demi langkah untuk memecahkan masalah atau
menyelesaikan suatu tugas. Kamus Besar Bahasa Indonesia (KBBI) mendefinisikan
algoritma sebagai urutan logis pengambilan keputusan untuk pemecahan
masalah.
Alat Bantu untuk
menuliskan Logika dan Algoritma, salah satunya adalah FLOWCHART.
menuliskan Logika dan Algoritma, salah satunya adalah FLOWCHART.
FLOWCHART
FLOWCHART adalah gambaran dalam
bentuk diagram alir dari algoritma dalam suatu program atau prosedur
sistem secara logika, yang menyatakan arah alur program dalam menyelesaikan
suatu masalah.
bentuk diagram alir dari algoritma dalam suatu program atau prosedur
sistem secara logika, yang menyatakan arah alur program dalam menyelesaikan
suatu masalah.
SIMBOL Flowchart
Pedoman-pedoman dalam
Membuat
Flowchart:
Flowchart:
- Bagan alir sebaiknya
digambar dari atas ke bawah dan mulai dari bagian kiri dari suatu halaman. - Kegiatan di dalam bagan
alir harus ditunjukkan dengan jelas. - Harus ditunjukkan dari
mana kegiatan akan dimulai dan dimana akan berakhirnya (diawali dari
satu titik START dan diakhiri dengan END). - Masing-masing kegiatan
di dalam bagan alir sebaiknya digunakan suatu kata yang mewakili suatu
pekerjaan, misalnya: - “Persiapkan”
dokumen - “Hitung”
gaji - Masing-masing kegiatan
di dalam bagan alir harus di dalam urutan yang semestinya. - Kegiatan yang terpotong
dan akan disambung di tempat lain harus ditunjukkan dengan jelas menggunakan
simbol penghubung. - Gunakanlah simbol-simbol
bagan alir yang standar.
Secara garis besar,
Ada 3 bagian utama dalam flowchart :
Ada 3 bagian utama dalam flowchart :
INPUT
PROSES
OUTPUT
Notasi Algoritma
heru768, Sunday, March 29, 2009
Sebelum membahas
masalah notasi algoritma, terlebih dahulu kita pahami pengertian-pengertian dan
konsep dasar seperti di bawah ini:
Algoritma : urutan langkah-langkah atau instruksi-instruksi yang harus dilaksanakan untuk memecahkan masalah.
Flowchart : (Diagram alur) adalah urutan instruksi-instruksi program yang digambarkan dalam bentuk suatu diagram.
Program : sederetan instruksi atau perintah (dalam bahasa yang di mengerti oleh komputer) untuk melaksanakan tugas-tugas tertentu, sehingga menghasilkan suatu keluaran / output yang diharapkan.
Bahasa pemrograman : program yang berisikan instruksi-instruksi yang dimengerti oleh komputer. Ada 2 klasifikasi dalam bahasa pemrograman, yaitu;
1. Low level language / bahasa tingkat rendah yang berorientasi pada mesin, contohnya: bahasa mesin / machine language dan bahasa rakitan / assembly language.
2. High level language /bahasa tingkat tinggi adalah bahasa pemrograman yang berorientasi pada manusia. Contohnya : BASIC, PASCAL, COBOL, FORTRAN, C.
Sebuah algoritma merupakan deskripsi pelaksanaan suatu proses, dimana algoritma disusun oleh sederetan langkah instruksi yang logis.
Kata logis merupakan kata kunci dalam sebuah algoritma. Langkah-langkah di dalam algoritma harus logis, ini berarti hasil dari urutan langkah-langkah tersebut harus dapat ditentukan, benar atau salah. Langkah-langkah yang tidak benar dapat memberikan hasil yang salah.
Sebagai contoh, tinjau persoalan mempertukarkan isi dua bejana, A dan B. Bejana A berisi larutan yang berwarna merah, sedangkan bejana B berisi air berwarna biru. Kita ingin mempertukarkan isi kedua bejana itu sedemikian sehingga bejana A berisi larutan berwarna biru dan bejana B berisi larutan berwarna merah. Untuk mempertukarkan isi dua bejana, kita memerlukan sebuah bejana tambahan yang diperlukan sebagai tempat penampungan sementara. Sebut bejana tambahan tersebut bejana C. Dengan menggunakan bejana bantu C ini, algoritma mempertukarkan isi dua buah bejana yang benar adalah sebagai berikut ini:
Deskripsi Algoritma Tukar Isi Bejana:
1. Tuangkan larutan dari bejana A ke dalam bejana C.
2. Tuangkan larutan dari bejana B ke dalam bejana A.
3. Tuangkan larutan dari bejana C ke dalam bejana B.
Dengan cara tersebut maka bejana A berisi larutan berwarna biru dan bejana B berisi larutan berwarna merah.
Oke…seteleh deskripsi tersebut mari kita langsung masuk ke materinya…..
Seperti disebutkan diatas, bahwa algoritma adalah urutan langkah-langkah atau instruksi-instruksi yang harus dilaksanakan untuk memecahkan masalah. Algoritma ini dituliskan dalam sebuah notasi yang disebut Notasi Algoritma. Notasi algoritma merupakan hal dasar yang harus diketahui oleh setiap orang yang ingin membuat suatu pogram, karena dalam notasi algoritma inilah terdapat kerangka-kerangka suatu program. Ciri notasi algoritma yang baik yaitu dapat diterjemahkan ke dalam berbagai bahasa pemrograman. Notasi algoritma bukan notasi bahasa pemrograman, sehingga siapapun dapat membuat notasi algoritma yang berbeda. Hal yang penting mengenai notasi tersebut adalah mudah dibaca dan dimengerti. Meskipun demikian untuk menghindari kekeliriuan, ketaatan terhadap notasi perlu diperhatikan. Di bawah ini ada 3 notasi yang umum digunakan dalam penulisan algoritma, yaitu :
1. Notasi Alami
2. Flowchart / Diagram Alur
3. Pseudo-Code (seperti kode)
1. NOTASI ALAMI
Penulisan algoritma dengan notasi alami adalah dengan cara menuliskan instruksi-instuksi yang harus dilaksanakan untuk memecahkan masalah dalam bentuk untaian kalimat deskriptif.
Dengan notasi bergaya kalimat ini, deskripsi setiap langkah dijelaskan dengan bahasa yang gamblang. Proses diawali dengan kata kerja seperti ‘baca’, ‘hitung’, ‘bagi’, ‘ganti’, dan sebagainya, sedangkan pernyataan kondisional dinyatakan dengan ‘jika…maka…’. Notasi ini bagus untuk algoritma yang pendek, namun untuk masalah yang algoritmanya besar, notasi ini jelas tidak efisien. Selain itu, pengkonversian notasi algoritma ke notasi bahasa pemrograman cenderung relative sukar.
2. FLOWCHART / DIAGRAM ALUR
Ada 2 jenis Flowchart :
a. flowchart sistem, adalah suatu gambar yang menjelaskan :
- file-file yang diproses oleh program
- jenis piranti yang digunakan oleh file
- operasi terhadap file (masukan ataupun keluaran).
b. flowchart program (biasa disebut flowchart saja), adalah suatu gambar yang menjelaskan urutan :
- Pembacaan data
- Pemrosesan data
- Pengambilan keputusan terhadap data
- Penyajian hasil pemrosesan data
Nah….yang kita bahas disini adalah flowchart program atau biasa disebut flowchart saja.
Flowchart/Diagram Alur popular pada awal-awal era pemrograman dengan komputer (terutama dengan bahasa Basic, Fortran, dan Cobol). Diagram alur lebih menggambarkan aliran instruksi di dalam program secara visual dibanding memperlihatkan struktur program. Notasi diagram alur lebih cocok digunakan untuk masalah yang kecil, untuk masalah yang besar tidak cocok digunakan karena membutuhkan berlembar halaman kertas. Selain itu, pengkonversian notasi algoritma ke bahasa pemrograman cenderung relatif sukar.
Simbol-simbol pada flowchart
Untuk mulai/akhir:
Algoritma : urutan langkah-langkah atau instruksi-instruksi yang harus dilaksanakan untuk memecahkan masalah.
Flowchart : (Diagram alur) adalah urutan instruksi-instruksi program yang digambarkan dalam bentuk suatu diagram.
Program : sederetan instruksi atau perintah (dalam bahasa yang di mengerti oleh komputer) untuk melaksanakan tugas-tugas tertentu, sehingga menghasilkan suatu keluaran / output yang diharapkan.
Bahasa pemrograman : program yang berisikan instruksi-instruksi yang dimengerti oleh komputer. Ada 2 klasifikasi dalam bahasa pemrograman, yaitu;
1. Low level language / bahasa tingkat rendah yang berorientasi pada mesin, contohnya: bahasa mesin / machine language dan bahasa rakitan / assembly language.
2. High level language /bahasa tingkat tinggi adalah bahasa pemrograman yang berorientasi pada manusia. Contohnya : BASIC, PASCAL, COBOL, FORTRAN, C.
Sebuah algoritma merupakan deskripsi pelaksanaan suatu proses, dimana algoritma disusun oleh sederetan langkah instruksi yang logis.
Kata logis merupakan kata kunci dalam sebuah algoritma. Langkah-langkah di dalam algoritma harus logis, ini berarti hasil dari urutan langkah-langkah tersebut harus dapat ditentukan, benar atau salah. Langkah-langkah yang tidak benar dapat memberikan hasil yang salah.
Sebagai contoh, tinjau persoalan mempertukarkan isi dua bejana, A dan B. Bejana A berisi larutan yang berwarna merah, sedangkan bejana B berisi air berwarna biru. Kita ingin mempertukarkan isi kedua bejana itu sedemikian sehingga bejana A berisi larutan berwarna biru dan bejana B berisi larutan berwarna merah. Untuk mempertukarkan isi dua bejana, kita memerlukan sebuah bejana tambahan yang diperlukan sebagai tempat penampungan sementara. Sebut bejana tambahan tersebut bejana C. Dengan menggunakan bejana bantu C ini, algoritma mempertukarkan isi dua buah bejana yang benar adalah sebagai berikut ini:
Deskripsi Algoritma Tukar Isi Bejana:
1. Tuangkan larutan dari bejana A ke dalam bejana C.
2. Tuangkan larutan dari bejana B ke dalam bejana A.
3. Tuangkan larutan dari bejana C ke dalam bejana B.
Dengan cara tersebut maka bejana A berisi larutan berwarna biru dan bejana B berisi larutan berwarna merah.
Oke…seteleh deskripsi tersebut mari kita langsung masuk ke materinya…..
Seperti disebutkan diatas, bahwa algoritma adalah urutan langkah-langkah atau instruksi-instruksi yang harus dilaksanakan untuk memecahkan masalah. Algoritma ini dituliskan dalam sebuah notasi yang disebut Notasi Algoritma. Notasi algoritma merupakan hal dasar yang harus diketahui oleh setiap orang yang ingin membuat suatu pogram, karena dalam notasi algoritma inilah terdapat kerangka-kerangka suatu program. Ciri notasi algoritma yang baik yaitu dapat diterjemahkan ke dalam berbagai bahasa pemrograman. Notasi algoritma bukan notasi bahasa pemrograman, sehingga siapapun dapat membuat notasi algoritma yang berbeda. Hal yang penting mengenai notasi tersebut adalah mudah dibaca dan dimengerti. Meskipun demikian untuk menghindari kekeliriuan, ketaatan terhadap notasi perlu diperhatikan. Di bawah ini ada 3 notasi yang umum digunakan dalam penulisan algoritma, yaitu :
1. Notasi Alami
2. Flowchart / Diagram Alur
3. Pseudo-Code (seperti kode)
1. NOTASI ALAMI
Penulisan algoritma dengan notasi alami adalah dengan cara menuliskan instruksi-instuksi yang harus dilaksanakan untuk memecahkan masalah dalam bentuk untaian kalimat deskriptif.
Dengan notasi bergaya kalimat ini, deskripsi setiap langkah dijelaskan dengan bahasa yang gamblang. Proses diawali dengan kata kerja seperti ‘baca’, ‘hitung’, ‘bagi’, ‘ganti’, dan sebagainya, sedangkan pernyataan kondisional dinyatakan dengan ‘jika…maka…’. Notasi ini bagus untuk algoritma yang pendek, namun untuk masalah yang algoritmanya besar, notasi ini jelas tidak efisien. Selain itu, pengkonversian notasi algoritma ke notasi bahasa pemrograman cenderung relative sukar.
2. FLOWCHART / DIAGRAM ALUR
Ada 2 jenis Flowchart :
a. flowchart sistem, adalah suatu gambar yang menjelaskan :
- file-file yang diproses oleh program
- jenis piranti yang digunakan oleh file
- operasi terhadap file (masukan ataupun keluaran).
b. flowchart program (biasa disebut flowchart saja), adalah suatu gambar yang menjelaskan urutan :
- Pembacaan data
- Pemrosesan data
- Pengambilan keputusan terhadap data
- Penyajian hasil pemrosesan data
Nah….yang kita bahas disini adalah flowchart program atau biasa disebut flowchart saja.
Flowchart/Diagram Alur popular pada awal-awal era pemrograman dengan komputer (terutama dengan bahasa Basic, Fortran, dan Cobol). Diagram alur lebih menggambarkan aliran instruksi di dalam program secara visual dibanding memperlihatkan struktur program. Notasi diagram alur lebih cocok digunakan untuk masalah yang kecil, untuk masalah yang besar tidak cocok digunakan karena membutuhkan berlembar halaman kertas. Selain itu, pengkonversian notasi algoritma ke bahasa pemrograman cenderung relatif sukar.
Simbol-simbol pada flowchart
Untuk mulai/akhir:
Simbol ini dinamakan
terminator, digunakan untuk menyatakan MULAI (START) dan SELESAI (END) suatu
algoritma.Untuk input:
Manual input
merupakan KOTAK MASUKAN yang digunakan untuk membaca data yang diberikan oleh
usernya. Jadi user mengimput suatu harga/variable/nilai.Data merupakan KOTAK
DATA yang digunakan untuk membaca dan menampilkan data. Contoh aplikasinya
yaitu jika kita ingin kita ingin mengetahui saldo tabungan kita pada mesin ATM,
ATM hanya tinggal membaca data yang ada.Untuk Proses:
Proses merupakan
KOTAK PENUGASAN untuk melakukan perhitungan matematika yang hasilnya diberikan
sebagai suatu variable.Decision merupakan
KOTAK KEPUTUSAN untuk memutuskan arah atau percabangan yang diambil sesuai
dengan kondisi yang saat itu terjadi. Hanya ada 2 keputusan yaitu BENAR atau
SALAH.Untuk Output:
Kotak ini selain untuk input, digunakan juga
untuk output. Digunakan untuk menampilkan data.Dokumen merupakan
KOTAK KELUARAN untuk menampilkan / mencetak / menyimpan hasil(keluaran).Simbol-simbol lain yang digunakan antara lain:
Simbol Aliran Panah.Connector merupakan
SIMBOL PENGHUBUNG, untuk penghubung bila diagram alur terputus tapi masih dalam
halaman yang sama.Off-page connector
merupakan SIMBOL PENGHUBUNG, untuk penghubung bila diagram alur terputus
disebabkan misalnya oleh pergantian halaman (tak cukup digambar 1 halaman).3. PSEUDO-CODE
Pseudo-code adalah notasi yang menyerupai notasi bahasa pemrograman tingkat tinggi, khususnya Pascal dan C. Bahasa pemrograman umumnya mempunyai notasi yang hampir mirip untuk beberapa instruksi seperti notasi if-then-else, while-do, repeat-until, read, write, dan sebagainya. Namun tidak seperti bahasa pemrograman yang direpotkan dengan tanda titik koma, indeks, format keluaran, kata-kata khusus, dan sebagainya, sembarang versi Pseudo-code dapat diterima asalakan perintahnya tidak membingungkan pembaca. Keuntungan menggunakan notasi Pseudo-code adalah kemudahan mentranslasi ke notasi bahasa pemrograman, karena terdapat korespodensi antara setiap Pseudo-code dengan notasi bahasa pemrograman. Sehingga Pseudo-code cocok untuk algoritma yang rumit.
CONTOH KASUS
Buatlah algoritma untuk menghitung luas persegi panjang dengan ketiga notasi algoritma diatas?
Jawab.
1. Notasi Alami
- Dapatkan nilai panjang
- Dapatkan nilai lebar
- Kalikan nilai panjang dengan nilai lebar dan berikan nilainya kehasil
- Tampilkan nilai hasil
2. Flowchart
3. Pseudo-code
p, l, ls : numeric
begin
read (p, l)
ls : p x l
print (ls)
end.
Algoritma-algoritma yang merupakan
konsep Pre-emptive
Filed Under:
1. Penjadwalan
Round-Robin (RR)
semua proses dianggap penting dan di beri jatah waktu pemroses yang disebut kwanta. Proses berjalan dieksekusi oleh pemproses sebanyak saru kwanta, kemudian penjadwal akan megalihkan ke proses berikutnya juga untuk berjalan satu kwanta, kemudian dilanjutkan ke proses berikutnya, juga diproses satu kwanta, begitu setersnya sampai kembali ke proses awal dan berulang.
Ketentuan penjadwalan ini adalah sebagai berikut :
semua proses dianggap penting dan di beri jatah waktu pemroses yang disebut kwanta. Proses berjalan dieksekusi oleh pemproses sebanyak saru kwanta, kemudian penjadwal akan megalihkan ke proses berikutnya juga untuk berjalan satu kwanta, kemudian dilanjutkan ke proses berikutnya, juga diproses satu kwanta, begitu setersnya sampai kembali ke proses awal dan berulang.
Ketentuan penjadwalan ini adalah sebagai berikut :
- Bila kwanta gabis dan proses belum selesai maka
proses running itu menjadi ready dan prmroses dialihkan ke proses lain,
- Jika kwanta belum habis dan proses menuggu suatu
kejadian (misalnya menunggu suatu proses I/O)
- JIka kwanta belum habis dan proses menunggu suatu
kejadian (misalnya menunggu suatu operasi I/O) maka proses running itu
pemroses di alihkan ke proses lain.
2. Multiple Feedback
Queues (MPQ)
Sasaran Penjadwalan ini untuk meminimalkan banyaknya swapping baru yang dilakukan adalah :
Sasaran Penjadwalan ini untuk meminimalkan banyaknya swapping baru yang dilakukan adalah :
- Proses yang sangat banyak menggunakan pemroses
diberi jatah waktu lebih banyak (kwanta lebih besar) dan satu waktu.
- Penjadwalan dilakukan berdasarkan kelas-kelas
prioritas proses kelas tertinggi berjalan selama satu kwanta, kelas berikutnya
berjalan dua kwanta, kolom berikutnya berjalan tiga kwanta dan seterusnya.
Ketentuan penjadwalan
ini adalah sebagai berikut :
Jalankan proses-proses pada kelas prioritas tertinggi
Jika Proses telah menggunakan seluruh kwanta yang diberikan prioritasnya diturunkan satu kelas
Proses yang masuk pertama kali ke sistem diberi prioritas tertinggi.
3. Sortest-Remaind-First (SRF)
Penjadwalan yang memprioritaskan estimasi waktu proses yang rendah. ketentuannya yaitu proses-proses yang di estimasi memiliki sisa waktu. Proses terendah segera dieksekusi termasuk proses-proses yang baru masuk dalam antrian.
4. Hightes-Ratio-Next (HRN)
Penjadwalan yang memprioritaskan "Rasio prioritas dinamis" tertinggi.
dimana HRN di hitung dengan rumus :
Prioritas = (waktu tinggi+waktu layanan)/waktu layanann
5. Priority Schedule (PS)
Penjadwalan yang memprioritaskan proses yang memiliki prioritas statis tertinggi.
6. Guaranteed Schedule (GS)
Penjadwalan ini berupaya memberi masing-masing daya pemroses yang sama, jika terdapat N proses maka tiap proses diberikan 1/n daya pemroses.
Jalankan proses-proses pada kelas prioritas tertinggi
Jika Proses telah menggunakan seluruh kwanta yang diberikan prioritasnya diturunkan satu kelas
Proses yang masuk pertama kali ke sistem diberi prioritas tertinggi.
3. Sortest-Remaind-First (SRF)
Penjadwalan yang memprioritaskan estimasi waktu proses yang rendah. ketentuannya yaitu proses-proses yang di estimasi memiliki sisa waktu. Proses terendah segera dieksekusi termasuk proses-proses yang baru masuk dalam antrian.
4. Hightes-Ratio-Next (HRN)
Penjadwalan yang memprioritaskan "Rasio prioritas dinamis" tertinggi.
dimana HRN di hitung dengan rumus :
Prioritas = (waktu tinggi+waktu layanan)/waktu layanann
5. Priority Schedule (PS)
Penjadwalan yang memprioritaskan proses yang memiliki prioritas statis tertinggi.
6. Guaranteed Schedule (GS)
Penjadwalan ini berupaya memberi masing-masing daya pemroses yang sama, jika terdapat N proses maka tiap proses diberikan 1/n daya pemroses.
PENGERTIAN DASAR LOGIKA
DAN ALGORITMA
Diperkenalkan Oleh
Ahli atematika : Abu Ja’far Muhammad Ibnu Musa Al Khawarizmi
DEFINISI ALGORITMA
1. Langkah-langkah
yang dilakukan agar solusi masalah dapat diperoleh
2. Suatu prosedur yang merupakan urutan langkah-langkah yang terintegrasi
3. Suatu metode khusus yang digunakan untuk menyelesaikan suatu masalah yang nyata
2. Suatu prosedur yang merupakan urutan langkah-langkah yang terintegrasi
3. Suatu metode khusus yang digunakan untuk menyelesaikan suatu masalah yang nyata
Kriteria pemilihan
Algoritma
1. Ada output
2. Efektifitas dan Efesiensi
3. Jumlah langkahnya berhingga
4. Berakhir
5. Terstruktur
1. Ada output
2. Efektifitas dan Efesiensi
3. Jumlah langkahnya berhingga
4. Berakhir
5. Terstruktur
“Suatu Algoritma yang
terbaik yaitu Algoritma yang menghasilkan output yang tepat guna (efektif)
dalam waktu yang relatif singkat dan penggunaan memori yang relatif sedikit
(efisien) dengan langkah yang berhingga dan prosedurnya berakhir baik dalam
keadaan diperoleh suatu solusi ataupun tidak adanya solusi “
Tahapan Analisa
Algoritma
1. Merencanakan
Algoritma
2. Menyatakan
Algoritma
a. Bahasa semu/
sehari-hari (pseucode)
b. Diagram Alur / Flowchart
c. Statement/ penggalan program
b. Diagram Alur / Flowchart
c. Statement/ penggalan program
3. Validitas
Algoritma
4. Menganalisa
Algoritma
a. Waktu Tempuh/
Running Time
i. Banyaknya langkah
ii. Bear dab jenis input data
iii. Jenis operasi
iv. Komputer dan kompilator
ii. Bear dab jenis input data
iii. Jenis operasi
iv. Komputer dan kompilator
b. Jumlah memori yang
digunakan
5. Menguji Algoritma
a. Fase Debugging
b. Fase Profillig
b. Fase Profillig
Sifat-sifat Algoritma
1. Banyaknya langkah
intruksi harus berhingga
2. Langkah atau intruksi harus jelas
3. Proses harus jelas dan mempunyai batasan
4. Input dan Output harus mempunyai batasan
5. Efektifitas
6. Adanya bataan ruang lingkup.
2. Langkah atau intruksi harus jelas
3. Proses harus jelas dan mempunyai batasan
4. Input dan Output harus mempunyai batasan
5. Efektifitas
6. Adanya bataan ruang lingkup.
Pada algoritma klasik, diterapkan teknik enkripsi konvensional (simetris). Algoritma ini merupakan algoritma kriptografi yang biasa digunakan orang sejak berabad-abad yang lalu. Dua teknik dasar yang biasa digunakan, yaitu : [KUR04]
1. Teknik Subsitusi
2. Teknik Transposisi
1. Teknik Subsitusi
Subsitusi adalah penggantian setiap karakter plaintext dengan karakter lain. Beberapa istilah yang mungkin perlu diingat adalah : [KUR04]
a. Monoalfabet : Setiap karakter ciphertext mengganti satu macam karakter plaintext tertentu.
b. Polyalfabet : Setiap karakter ciphertext dapat mengganti lebih dari satu karakter plaintext.
c. Monograf / unilateral : Satu enkripsi dilakukan terhadap satu karakter plaintext.
d. Polygraf / multilateral : Satu enkripsi dilakukan terhadap lebih dari satu karakter plaintext sekaligus.
Cipher subsitusi paling tua yang dikenal adalah subsitusi yang dilakukan Julius Caesar. Beberapa teknik subsitusi yang pernah dilakukan, antara lain : [KUR04]
a. Subsitusi deret campuran kata kunci yaitu subsitusi yang kata kuncinya didapat dari mengumpulkan karakter yang sama dari sebuah plaintext dan pada ciphertextnya ditambahkan semua sisa karakter dalam abjad.
b.bSubsitusi monomer-dinome-trinome. Monome berarti setiap satu karakter plaintext akan disubsitusi oleh satu karakter ciphertext, dinome disubsitusi dua karakter ciphertext, tridome disubsitusi tiga karakter ciphertext. Jadi sistem ini adalah campuran dari ketiga sistem dasar.
c. Subsitusi multilateral variant. Subsitusi ini masih termasuk jenis monoalfabet yang dalam mensubsitusi memanfaatkan huruf abjad a,b,c,…,z yang disusun dalam matrik 5 X 5.
d. Subsitusi digrafik. Pada sistem ini, setiap huruf plaintext akan disubsitusi oleh dua huruf ciphertext. Pola huruf cipher text diambil dari sebuah matrik 26 X 26 yang berasal dari 26 abjad yang memiliki pola khusus.
e. Subsitusi persegi panjang. Sistem digrafik terlalu memerlukan matrik yang besar. Untuk memperkecil matrik dengan keamanan yang setara dapat digunakan sistem empat persegi.
f. Subsitusi kode playfair. Kode rahasia multi huruf yang paling terkenal adalah playfair. Playfair menggunakan 676 digraf. Selama waktu yang lama, kode ini dianggap tak dapat dipecahkan. Playfair dijadikan sistem standar oleh tentara Inggris dalam PD I dan masih digunakan secara luas oleh tentara Amerika dan sekutu selama PD II. Sistem ini menggunakan matrik 5 X 5.
g. Subsitusi Polialfabet periodik. Dalam sistem polialfabet, setiap ciphertext dapat memiliki banyak kemungkinan plaintext. Dan sistem periodik itu sendiri dikarenakan adanya kunci yang berulang. Jenis polialfabet klasik yang terkenal adalah Vigenere.
h. Enigma. Merupakan mesin kriptografi yang digunakan oleh tentara NAZI Hitler pada masa PD II. Mesin ini menggunakan rotor. Enigma menggunakan tiga rotor untuk melakukan subsitusi. Tiga rotor berarti tiga kali subsitusi.
2. Teknik Transposisi ( Permutasi )
Beberapa model kriptografi yang menggunakan teknik transposisi, antara lain : [KUR04]
1. Algoritma transposisi kolom dengan kunci numerik. Teknik ini menggunakan permutasi karakter. Kunci dapat diperoleh dari kata yang mudah dibaca dan kemudian dikodekan menjadi bilangan.
2. Masukan plaintext pola zig-zag, keluaran ciphertext berupa baris.
3. Masukan pola segitiga, keluaran berupa kolom, dibaca dari atas kebawah.
4. Masukan berpola spiral, dari luar kedalam, keluaran berupa kolom dibaca dari atas ke bawah.
5. Dimasukan secara diagonal dari kiri bawah ke kanan atas, keluaran baris.
6. Masukan spiral dari dalam ke luar, keluaran diagonal bergantian.
Kombinasi subsitusi dan transposisi yang komplek menjadi dasar pembentukan algoritma-algoritma kriptografi modern. Salah satu algoritma klasik yang menggunakan kedua teknik ini adalah VIC yang tidak memerlukan komputer dalam penggunaannya.
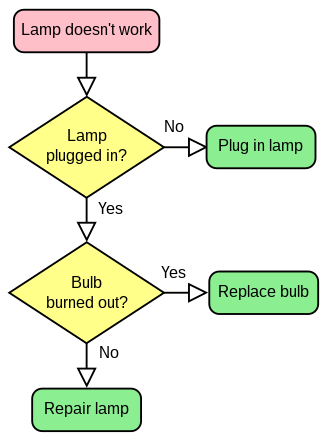
Diagram Alur sering digunakan untuk
menggambarkan sebuah algoritma.
Dalam matematika dan komputasi, algoritma merupakan kumpulan perintah untuk
menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara
bertahap dari awal hingga akhir. Masalah tersebut dapat berupa apa saja, dengan
catatan untuk setiap masalah, ada kriteria kondisi awal yang harus dipenuhi
sebelum menjalankan algoritma. Algoritma akan dapat selalu berakhir untuk semua
kondisi awal yang memenuhi kriteria, dalam hal ini berbeda dengan heuristik.
Algoritma sering mempunyai langkah pengulangan (iterasi)
atau memerlukan keputusan (logika Boolean danperbandingan)
sampai tugasnya selesai.
Desain dan analisis algoritma adalah suatu cabang khusus dalam ilmu
komputer yang mempelajari karakteristik dan performa dari suatu
algoritma dalam menyelesaikan masalah, terlepas dari implementasi algoritma
tersebut. Dalam cabang disiplin ini algoritma dipelajari secara abstrak, terlepas
dari sistem komputer atau bahasa pemrograman yang
digunakan. Algoritma yang berbeda dapat diterapkan pada suatu masalah dengan
kriteria yang sama.
Kompleksitas dari suatu algoritma merupakan ukuran seberapa banyak
komputasi yang dibutuhkan algoritma tersebut untuk menyelesaikan masalah.
Secara informal, algoritma yang dapat menyelesaikan suatu permasalahan dalam
waktu yang singkat memiliki kompleksitas yang rendah, sementara algoritma yang
membutuhkan waktu lama untuk menyelesaikan masalahnya mempunyai kompleksitas
yang tinggi.
SEJARAH ISTILAH “ALGORITMA”
Kata algoritma berasal dari latinisasi nama
seorang ahli matematika dari Uzbekistan Al KhawÄrizmi (hidup sekitar abad ke-9),
sebagaimana tercantum pada terjemahan karyanya dalam bahasa latin dari abad
ke-12 “Algorithmi de numero Indorum”. Pada awalnya kata algorisma adalah istilah yang merujuk
kepada aturan-aturan aritmetis untuk menyelesaikan persoalan dengan menggunakan
bilangan numerik arab (sebenarnya dari India, seperti tertulis pada judul di
atas). Pada abad ke-18, istilah ini berkembang menjadialgoritma, yang mencakup semua prosedur
atau urutan langkah yang jelas dan diperlukan untuk menyelesaikan suatu
permasalahan.
JENIS-JENIS
ALGORITMA
Terdapat beragam
klasifikasi algoritma dan setiap klasifikasi mempunyai
alasan tersendiri. Salah satu cara untuk melakukan klasifikasi jenis-jenis
algoritma adalah dengan memperhatikan paradigma dan metode yang digunakan untuk
mendesain algoritma tersebut. Beberapa paradigma yang digunakan dalam menyusun
suatu algoritma akan dipaparkan dibagian ini. Masing-masing paradigma dapat
digunakan dalam banyak algoritma yang berbeda.
- Divide and Conquer,
paradigma untuk membagi suatu
permasalahan besar menjadi permasalahan-permasalahan yang lebih kecil.
Pembagian masalah ini dilakukan terus menerus sampai ditemukan bagian
masalah kecil yang mudah untukdipecahkan.
Singkatnya menyelesaikan keseluruhan masalah dengan membagi masalah besar dan kemudian memecahkanpermasalahan-permasalahan kecil yang terbentuk.
- Dynamic programming,
paradigma pemrograman dinamik akan sesuai jika digunakan pada suatu
masalah yang mengandungsub-struktur yang optimal (, dan
mengandung beberapa bagian
permasalahan yang tumpang tindih .
Paradigma ini sekilas terlihat mirip dengan paradigma Divide and Conquer,
sama-sama mencoba untuk membagi permasalahan menjadi sub permasalahan yang
lebih kecil, tapi secara intrinsik ada perbedaan dari karakter
permasalahan yang dihadapi.
- Metode serakah. Sebuah algoritma serakah mirip
dengan sebuah Pemrograman dinamik,
bedanya jawaban dari submasalah tidak perlu diketahui dalam setiap tahap;
dan menggunakan pilihan “serakah” apa yang dilihat terbaik pada saat itu.
Algoritma untuk
menentukan sebuah bilangan yang kelipatanya 3,5,dan7 atau bukan !!!
- Jika suatu bilangan dibagi angka 3, menghasilkan
bilangan bulat, maka bilangan tersebut adlah kelipatan 3.
- Jika suatu bilangan dibagi angka 3, menghasilkan
bilangan desimal, maka bilangan tersebut adlah bukan kelipatan 3.
- Jika suatu bilangan dibagi angka 5, menghasilkan
bilangan bulat, maka bilangan tersebut adlah kelipatan 5.
- Jika suatu bilangan dibagi angka 5, menghasilkan
bilangan desimal, maka bilangan tersebut adlah bukan kelipatan 5.
- Jika suatu bilangan dibagi angka 7, menghasilkan
bilangan bulat, maka bilangan tersebut adlah kelipatan 7.
- Jika suatu bilangan dibagi angka 7, menghasilkan
bilangan desimal, maka bilangan tersebut adlah bukan kelipatan 7.
contoh : p adalah
input
q adalah bil. bulat
r adalah bil. desimal
1. Jika p dibagi 3
menghasilkan q, maka p adalah kelipatan 3.
2. Jika p dibagi 3
menghasilkan r, maka p adalah bukan kelipatan 3.
Di dalam bahasa C ada
tiga file stream yang diberikan, yaitu stdin, stdout, dan stderr. Stdin
langsung terhubung dengan keyboard, sedangkan stdout dan stderr langsung
memunculkan pesan error ke layar.
Contoh penggunaan
stdout adalah printf. Penggunaan stdin contohnya adalah scanf.
Header yang ada pada
bahasa C merupakan suatu ‘bank’ dari fungsi-fungsi yang akan digunakan.
Tanpanya fungsi tidak bisa berjalan dengan baik.
Mendapatkan Input
dari Pemakai
Mendapatkan input
dari pemakai bisa menggunakan getchar() dan getc().
Funsi getc()
Sintaks untuk fungsi
getc adalah:
#include
int getc(FILE
*stream);
Contoh:
1: /* membaca input
dengan fungsi getc() */
2: #include
3:
4: main()
5: {
6: int c;
7: printf(”Ketik
salah satu karakter:\n”);
8: c = getc(stdin);
9: printf(”karakter
yang anda masukkan adalah: %c\n”, c);
10: fflush(stdin);
11: getchar();
12: return (0);
13: }
Setelah saya buat,
hasilnya seperti ini:
Dari contoh diatas,
kita pelajari bahwa apapun input yang kita masukkan akan berubah menjadi
karakter baik angka, huruf, dan simbol.
Funsi getchar()
Fungsi lainnya untuk
membaca input selain getc(stdin) adalah getchar().
Sintaks untuk fungsi
getchar adalah:
#include
int getchar(void);
Contoh:
1: #include
2: #include
3:
4: main()
5: {
6: int ch1, ch2;
7:
8: printf(”Masukkan 2
karakter :\n”);
9: ch1 = getc(stdin);
10: ch2 = getchar();
11: printf(”Karakter
pertama yang dimasukkan adalah: %c\n”, ch1);
12: printf(”Karakter
kedua yang dimasukkan adlaah %c\n”, ch2);
13:
14: fflush(stdin);
15: getch();
16: return 0;
17: }
Setelah saya buat,
hasilnya seperti ini:
Dari contoh diatas,
kita pelajari bahwa fungsi getchar() dan getc(stdin) memiliki fungsi yang sama,
yaitu untuk membaca input dari pemakai, baik angka, huruf, maupun simbol.
Menampilkan Output di
Layar dengan Fungsi putc() dan putchar()
Sintaks untuk fungsi
putc() adalah
#include
int putc(int c, FILE
*stream);
Contoh:
1: #include
2: #include
3:
4: main()
5: {
6: int ch;
7:
8: ch = 65;
9: printf(”The
character that has numeric value of 65 is:\n”);
10: putc(ch, stdout);
11:
12: getch();
13: return (0);
14: }
Setelah saya buat,
hasilnya seperti ini:
Fungsi putc()
digunakan untuk merubah suatu angka yang sudah terformat dalam memori menjadi
suatu karakter.
Sintaks untuk fungsi
putchar() adalah
#include
int putchar(int c);
Contoh:
1: #include
2: #include
3: main()
4: {
5: putchar(65);
6: putchar(10);
7: putchar(66);
8: putchar(10);
9: putchar(67);
10: putchar(10);
11: putchar(68);
12: putchar(10);
13: getch();
14: return (0);
15: }
Setelah saya buat,
hasilnya seperti ini:
Dalam fungsi
putchar() ini, fungsi ini tidak membutuhkan banyak argument-argumen, karena
angka yang ditulis sudah terdaftar dalam library stdout sehingga program hanya
perlu mencari angka yang sesuai dengan library yang ada dan memunculkannya
dalam bentuk karakter.
Menampilkan Pesan
dengan Fungsi printf()
Sintaks untuk fungsi
printf():
#include
int printf(const char
*format-string, …);
Untuk menampilkan
pesan dengan fungsi ini, kita perlu menggunakan tanda kutip dua, tanda persen
(%) dan variable yang ingin ditampilkan. Contohnya;
1: #include
2: main()
3:
4: {
5: int d;
6: d=40;
7: printf(”nilai d
adalah %d”,d);
8:
9: fflush(stdin);
10: getchar();
11: return 0;
12: }
Setelah dibuat,
hasilnya seperti ini:
Dari contoh diatas,
fungsi printf digunakan sebagai perintah untuk mencetak suatu pesan, hasil yang
ditampilkan (%d) adalah nilai yang terdapat dalam variabel D, dengan tipe
integer (d pada %d). Berikut ini adalah daftar format yang bisa digunakan
dengan fungsi printf():
%c
Untuk format karakter (huruf, symbol, angka, dsb).
Untuk format karakter (huruf, symbol, angka, dsb).
%d
Format integer untuk nilai.
Format integer untuk nilai.
%i
Format integer untuk nilai (sama dengan %d).
Format integer untuk nilai (sama dengan %d).
%f
Format integer tipe float untuk bilangan desimal (0.5, 0.7, 125.35)
Format integer tipe float untuk bilangan desimal (0.5, 0.7, 125.35)
%e
Format untuk notasi-notasi ilmiah (bentuk huruf kecil seperti e).
Format untuk notasi-notasi ilmiah (bentuk huruf kecil seperti e).
%E
Format untuk notasi-notasi ilmiah (bentuk huruf besar seperti E).
Format untuk notasi-notasi ilmiah (bentuk huruf besar seperti E).
%g
Penggunaan %f atau %e, kedua-duanya menghasilkan hasil yang lebih pendek.
Penggunaan %f atau %e, kedua-duanya menghasilkan hasil yang lebih pendek.
%G
Penggunaan %f atau %E, kedua-duanya menghasilkan hasil yang lebih pendek.
Penggunaan %f atau %E, kedua-duanya menghasilkan hasil yang lebih pendek.
%o
Format untuk oktal bertipe data unsigned.
Format untuk oktal bertipe data unsigned.
%s
Format untuk string.
Format untuk string.
%u
Format untuk integer bertipe data unsigned.
Format untuk integer bertipe data unsigned.
%x
Format untuk heksadesimal bertipe data unsigned (bentuk huruf kecil seperti x).
Format untuk heksadesimal bertipe data unsigned (bentuk huruf kecil seperti x).
%X
Format untuk heksadesimal bertipe data unsigned (bentuk huruf besar seperti X).
Format untuk heksadesimal bertipe data unsigned (bentuk huruf besar seperti X).
%p
Menampilkan argument yang ditunjuk pointer.
Menampilkan argument yang ditunjuk pointer.
%n
Mengingat jumlah karakter yang tertulis.
Mengingat jumlah karakter yang tertulis.
%%
Menampilkan tanda persen (%).
Menampilkan tanda persen (%).
Merubah Integer
Menjadi Angka-Angka Heksa
Untuk merubah suatu
integer menjadi bentuk heksa desimal, kita memerlukan %X (uppercase) atau %x
(lowercase) dalam suatu argumen. Contoh:
1: #include
2:
3: main()
4: {
5:
printf(”Hex(uppercase) Hex(lowercase) Decimal\n”);
6: printf(”%X %x
%d\n”, 0, 0, 0);
7: printf(”%X %x
%d\n”, 1, 1, 1);
8: printf(”%X %x
%d\n”, 2, 2, 2);
9: printf(”%X %x
%d\n”, 3, 3, 3);
10: printf(”%X %x
%d\n”, 4, 4, 4);
11: printf(”%X %x
%d\n”, 5, 5, 5);
12: printf(”%X %x
%d\n”, 6, 6, 6);
13: printf(”%X %x
%d\n”, 7, 7, 7);
14: printf(”%X %x
%d\n”, 8, 8, 8);
15: printf(”%X %x
%d\n”, 9, 9, 9);
16: printf(”%X %x
%d\n”, 10, 10, 10);
17: printf(”%X %x
%d\n”, 11, 11, 11);
18: printf(”%X %x
%d\n”, 12, 12, 12);
19: printf(”%X %x
%d\n”, 13, 13, 13);
20: printf(”%X %x
%d\n”, 14, 14, 14);
21: printf(”%X %x
%d\n”, 15, 15, 15);
22:
23: fflush(stdin);
24: getchar();
25: return(0);
26: }
Hasilnya seperti ini:
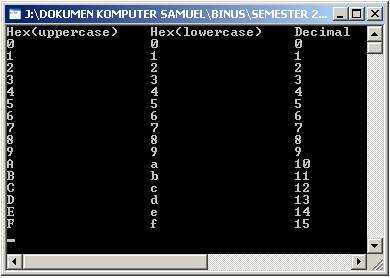
Menambahkan Lebar
Minimum
Contoh:
1: #include
2:
3: main()
4: {
5: int num1, num2;
6: num1 = 12;
7: num2 = 12345;
8: printf(”%d\n”,
num1);
9: printf(”%d\n”,
num2);
10: printf(”%5d\n”,
num1);
11: printf(”%05d\n”,
num1);
12: printf(”%2d\n”,
num2);
13:
14: fflush(stdin);
15: getchar();
16: return(0);
17: }
Setelah dibuat,
hasilnya seperti ini: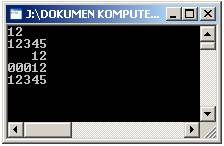
Pada hasil pertama
dan kedua, angka 12 dan 12345 tidak ditambahkan lebar minimum sehingga
posisinya tetap rata kiri sesuai besarnya input. Pada baris ketiga dan keempat
diatas, angka-angka ini mendapatkan penambahan minimum lebar sebanyak 5 slot
atau karakter. Sehingga keduanya menghasilkan rata kanan. Untuk hasil ke 4
karena ada slot yang kosong atau tidak diisi, maka yang kosong itu diberikan
nilai 0. Untuk hasil yang terakhir, diberikan lebar minimum 2 slot, tetapi
karena input yang diberikan melebihi yang ditetapkan, maka output yang
ditampilkan sebanyak input.
Output Rata Kiri dan
Rata Kanan
Contoh:
1: #include
2:
3: main()
4: {
5: int num1, num2,
num3, num4, num5;
6:
7: num1 = 1;
8: num2 = 12;
9: num3 = 123;
10: num4 = 1234;
11: num5 = 12345;
12:
13: printf(”%8d
%-8d\n”, num1, num1);
14: printf(”%8d
%-8d\n”, num2, num2);
15: printf(”%8d
%-8d\n”, num3, num3);
16: printf(”%8d
%-8d\n”, num4, num4);
17: printf(”%8d
%-8d\n”, num5, num5);
18:
19: getchar();
20: return 0;
21: }
Setelah dibuat,
hasilnya seperti ini:
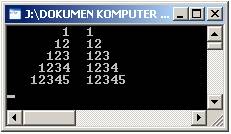
Kalau kita lihat pada
codingnya, ada %8d tanpa minus dan ada %-8d. Disini, tanda minus berfungsi
untuk mengeset karakter pada rata kiri, sedangkan yang tidak menggunakan tanda
minus berfungsi mengeset karakter pada rata kanan.
Mencetak Nilai dengan
Pembulatan
Contoh:
1: #include
2: main()
3: {
4: int int_num;
5: double flt_num;
6: int_num = 123;
7: flt_num =
123.456789;
8: printf(”Default
integer format : %d\n”, int_num);
9: printf(”With
precision specifier: %2.8d\n”, int_num);
10: printf(”Default
float format : %f\n”, flt_num);
11: printf(”With
precision specifier: %-10.2f\n”, flt_num); getchar();
12: return 0;
13: }
Setelah dibuat,
hasilnya seperti ini: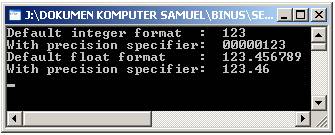
Seperti yang dijelaskan
pada bagian sebelumnya, hasil pertama yang menggunakan %d menampilkan karakter
dengan posisi rata kiri. Jika menggunakan %2.8d artinya tolong sediakan 8 slot
atau karakter, dengan 2 angka dibelakang koma. Sehingga bila ada slot yang
tidak diisi, maka yang tercetak adalah 0. Hasil ketiga merupakan contoh
bilangan jenis float secara umum. Jika ingin dibulatkan menjadi 2 angka
dibelakang koma (presisi) dengan rata kiri, maka kita perlu menambahkan tanda
minus (-) dan 2 di belakang titik berfungsi sebagai slot yang disediakan
dibelakang koma, yaitu sebanyak 2 slot.
Dikutip dari http://aelinik.free.fr/c/ch05.htm
Part 2 - Pemograman
& Coding
Ada 3 integer, 15,
150, dan 1500. Tulislah sebuah program yang mencetak integer di layar dalam
format heks!
Coding:
1: #include
2: #include
2: #include
3: int main()
4: {
5: int a, b, c;
4: {
5: int a, b, c;
6: printf(”masukkan
integer 1: “);
7: scanf(”%d”,&a);
8: printf(”\n”);
7: scanf(”%d”,&a);
8: printf(”\n”);
9: printf(”masukkan
integer 2: “);
10: scanf(”%d”,&b);
11: printf(”\n”);
10: scanf(”%d”,&b);
11: printf(”\n”);
12: printf(”masukkan
integer 3: “);
13: scanf(”\n%d”,&c);
14: printf(”\n”);
13: scanf(”\n%d”,&c);
14: printf(”\n”);
15: printf(”hex dari
integer 1 adalah %x\n”,a);
16: printf(”hex dari integer 2 adalah %x\n”,b);
17: printf(”hex dari integer 3 adalah %x\n”,c);
16: printf(”hex dari integer 2 adalah %x\n”,b);
17: printf(”hex dari integer 3 adalah %x\n”,c);
18: fflush(stdin);
19: getchar();
20: }
19: getchar();
20: }
Program: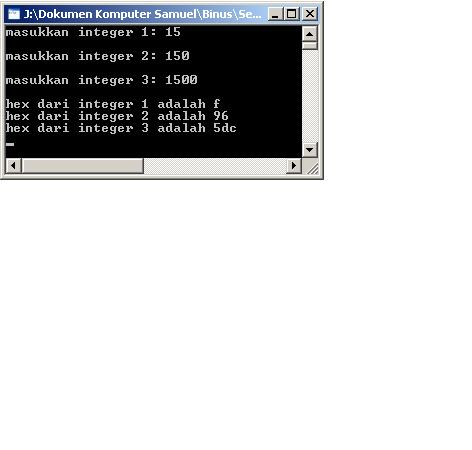
Graf
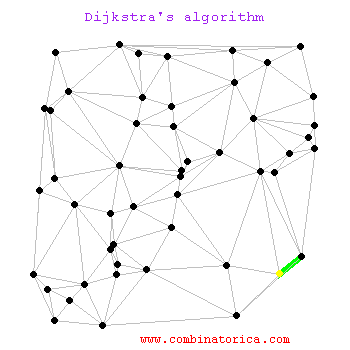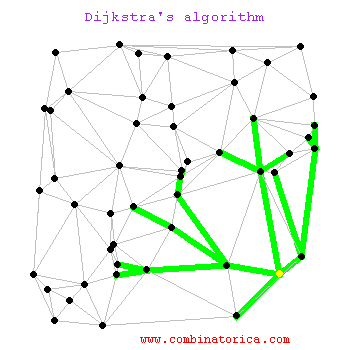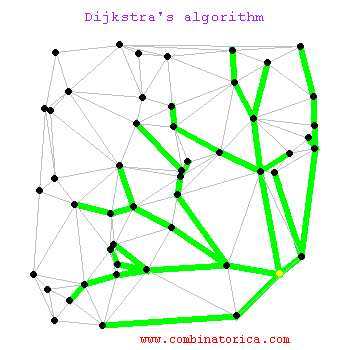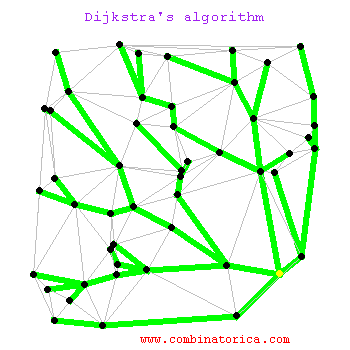
merupakan suatu cabang ilmu yang memiliki
banyak terapan. Banyak sekali struktur yang bisa direpresentasikan dengan graf,
dan banyak masalah yang bisa diselesaikan dengan bantuan graf. Seringkali graf
digunakan untuk merepresentasikan suaru jaringan. Misalkan jaringan jalan raya
dimodelkan graf dengan kota sebagai simpul (vertex/node) dan jalan yang menghubungkan
setiap kotanya sebagai sisi (edge) yang bobotnya (weight) adalah panjang dari jalan
tersebut.
Dalam beberapa model
persoalan dimungkinkan bahwa bobot dari suatu sisi bernilai negatif. Misalkan
simpul merepesentasikan bandara, sisi mereprentasikan penerbangan yang
memungkinkan, dan bobot dari setiap sisi adalah biaya yang dikeluarkan dalam
penerbangan tersebut. Untuk suatu kasus dimana seseorang akan dibayar untuk
menempuh rute tertentu oleh suatu biro penerbangan, maka bobotnya akan bernilai
negatif.
Lintasan terpendek
merupakan salah satu dari masalah yang dapat diselesaikan dengan graf. Jika
diberikan sebuah graf berbobot, masalah lintasan terpendek
adalah bagaimana kita mencari sebuah jalur pada graf yang meminimalkan jumlah
bobot sisi pembentuk jalur tersebut.
Terdapat beberapa macam persoalan lintasan terpendek antara lain:
Terdapat beberapa macam persoalan lintasan terpendek antara lain:
- Lintasan terpendek antara dua buah simpul
tertentu (a pair
shortets path).
- Lintasan terpendek antara semua pasangan simpul (all pairs shortest path).
- Lintasan terpendek dari simpul tertentu ke semua
simpul yang lain (single-source shoertest path).
- Lintasan terpendek antara dua buah simpul yang
melalui beberapa simpul tertentu (intermediate shortest path).
Algoritma Dijkstra,
dinamai menurut penemunya, Edsger Dijkstra, adalah
algoritma dengan prinsip greedy yang memecahkan masalah lintasan terpendek
untuk sebuah graf berarah dengan bobot sisi yang tidak negatif.
Algoritma Dijkstra
merupakan salah satu varian bentuk algoritma populer dalam pemecahan persoalan
yang terkait dengan masalah optimasi. Sifatnya sederhana dan lempang
(straightforward). Sesuai dengan arti greedy yang secara harafiah berarti tamak
atau rakus - namun tidak dalam konteks negatif -, algoritma greedy ini hanya
memikirkan solusi terbaik yang akan diambil pada setiap langkah tanpa
memikirkan konsekuensi ke depan. Prinsipnya, ambillah apa yang bisa Anda
dapatkan saat ini (take what you can get now!), dan keputusan yang telah
diambil pada setiap langkah tidak akan bisa diubah kembali. Intinya
Elemen-elemen
penyusun prinsip greedy pada Algoritma Dijkstra adalah :
1.Himpunan kandidat
Himpunan ini berisi elemen-elemen yang memiliki peluang untuk membentuk solusi. Pada persoalan lintasan terpendek dalam graf, himpunan kandidat ini adalah himpunan simpul pada graf tersebut.
Himpunan ini berisi elemen-elemen yang memiliki peluang untuk membentuk solusi. Pada persoalan lintasan terpendek dalam graf, himpunan kandidat ini adalah himpunan simpul pada graf tersebut.
2. Himpunan solusi
Himpunan ini berisi solusi dari permasalahan yang diselesaikan dan elemennya terdiri dari elemen dalam himpunan kandidat namun tidak semuanya atau dengan kata lain himpunan solusi ini adalah upabagian dari himpunan kandidat.
Himpunan ini berisi solusi dari permasalahan yang diselesaikan dan elemennya terdiri dari elemen dalam himpunan kandidat namun tidak semuanya atau dengan kata lain himpunan solusi ini adalah upabagian dari himpunan kandidat.
3. Fungsi seleksi
Fungsi seleksi adalah fungsi yang akan memilih setiap kandidat yang yang memungkinkan untuk menghasilkan solusi optimal pada setiap langkahnya.
Fungsi seleksi adalah fungsi yang akan memilih setiap kandidat yang yang memungkinkan untuk menghasilkan solusi optimal pada setiap langkahnya.
4. Fungsi kelayakan
Fungsi kelayakan akan memeriksa apakah suatu kandidat yang telah terpilih (terseleksi) melanggar constraint atau tidak. Apabila kandidat melanggar constraint maka kandidat tidak akan dimasukkan ke dalam himpunan solusi.
Fungsi kelayakan akan memeriksa apakah suatu kandidat yang telah terpilih (terseleksi) melanggar constraint atau tidak. Apabila kandidat melanggar constraint maka kandidat tidak akan dimasukkan ke dalam himpunan solusi.
5. Fungsi objektif
Fungsi objektif akan memaksimalkan atau meminimalkan nilai solusi. Tujuannya adalah memilih satu saja solusi terbaik dari masing-masing anggota himpunan solusi.
Fungsi objektif akan memaksimalkan atau meminimalkan nilai solusi. Tujuannya adalah memilih satu saja solusi terbaik dari masing-masing anggota himpunan solusi.
Ada beberapa kasus
pencarian lintasan terpendek yang diselesaikan menggunakan algoritma Dijkstra,
yaitu: pencarian lintasan terpendek antara dua buah simpul tertentu (a pair shortest path), pencarian lintasan terpendek
antara semua pasangan simpul (all pairs shortest path), pencarian lintasan terpendek
dari simpul tertentu ke semua simpul yang lain (single-source
shortest path), serta pencarian
lintasan terpendek antara dua buah simpul yang melalui beberapa simpul tertentu
(intermediate shortest path).
Pseudocode
procedure
Dijkstra(INPUT m: matriks, a : simpul awal)
{
Mencari lintasan terpendek dari simpul awal a ke semua simpul lainnya.
Masukan: matriks ketetanggaan (m) dari graf berbobot G dan simpul awal a
Keluaran: lintasan terpendek dari ake semua simpul lainnya
}
Kamus:
s : array [1..n] of integer
d : array [1..n] of integer
i : integer
Algoritma:
{ Langkah 0 (inisialisasi: }
traversal [1..n]
si <- 0
di <- mai
{
Mencari lintasan terpendek dari simpul awal a ke semua simpul lainnya.
Masukan: matriks ketetanggaan (m) dari graf berbobot G dan simpul awal a
Keluaran: lintasan terpendek dari ake semua simpul lainnya
}
Kamus:
s : array [1..n] of integer
d : array [1..n] of integer
i : integer
Algoritma:
{ Langkah 0 (inisialisasi: }
traversal [1..n]
si <- 0
di <- mai
{ Langkah 1: }
sa <- 1
da <- 8
{ Langkah 2, 3, …, n-1: }
traversal [2..n-1]
cari j sedemikian sehingga sj= 0
dan
dj = min {d1, d2, …, dn}
sj <- 1 {simpul j sudah terpilih}
perbarui di, untuk i = 1, 2, 3,
s.d. n dengan:
di(baru) = min{di(lama),dj+ mji}
sa <- 1
da <- 8
{ Langkah 2, 3, …, n-1: }
traversal [2..n-1]
cari j sedemikian sehingga sj= 0
dan
dj = min {d1, d2, …, dn}
sj <- 1 {simpul j sudah terpilih}
perbarui di, untuk i = 1, 2, 3,
s.d. n dengan:
di(baru) = min{di(lama),dj+ mji}
Kompleksitas waktu
algoritma (Running time) :
- Algoritma Dijkstra’menggunakan waktu sebesar
O(V*log V + E)di mana V dan E adalah banyaknya sisi dan titik.
- Kompleksitas algoritma Dijkstra adalah O(n2).
Sehingga, untuk mencari semua pasangan simpul terpendek, total waktu
asimptotik komputasinya adalah: T(n) = n.O(n2) = O(n3).
- Algoritma dijkstra lebih menguntungkan dari
sisirunning time
Dasar-Dasar Algortima Pemograman
Algoritma merupakan suatu metode khusus yang tepat dan terdiri dari serangkaian langkah ya/ng terstruktur dan dituliskan secara sistematis, yang akan dikerjakan untuk menyelesaikan suatu masalah dengan bantuan komputer.
Program adalah kata, ekspresi, pernyataan atau kombinasinya yang disusun dan dirangkai menjadi satu kesatuan prosedur yang berupa urutan langkah untuk menyelesaikan masalah yang diimplementasikan dengan menggunakan bahasa pemrograman sehingga dapat dieksekusi oleh komputer.
Pemrograman merupakan proses mengimplementasikan urutan langkah untuk menyelesaikan suatu masalah dengan menggunakan suatu bahasa pemrograman.
Pemrogram / Programer adalah orang yang bekerja menyusun suatu program.
Kriteria Programer yang baik:
>> Mampu menyusun algoritma dengan baik
>> Menguasai bahasa dan teknik penulisan program dengan baik
>> Dapat bekerja sama dalam suatu tim kerja
>> Dapat bekerja secara efisien dan tepat waktu
Dalam proses pembuatan Program, ada bebarapa tahapan yang harus dilakukan yaitu :
1. Definisi masalah
2. Analisis kebutuhan
3. Penyusunan algoritma
4. Pemrograman
5. Testing dan Debugging
6. Dokumentasi
7. Pemeliharaan